WHY SYSTEM MODELS?
- Do you know early on if the requirements can be reached?
- Are you sure that the optimization potential justifies the effort?
- What are the key performance parameters and what drives them?
- Can I derive degradation states in my machines?
- Do you want to go beyond counting operation hours in Industry 4.0?
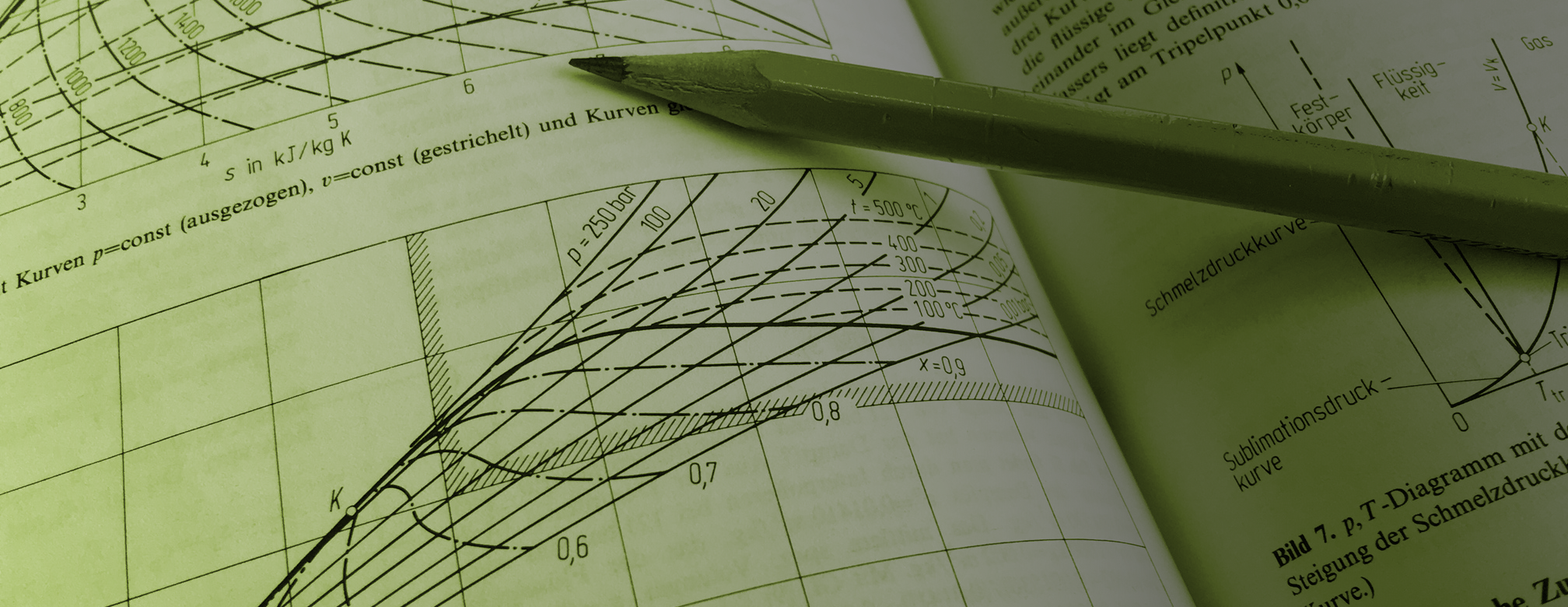
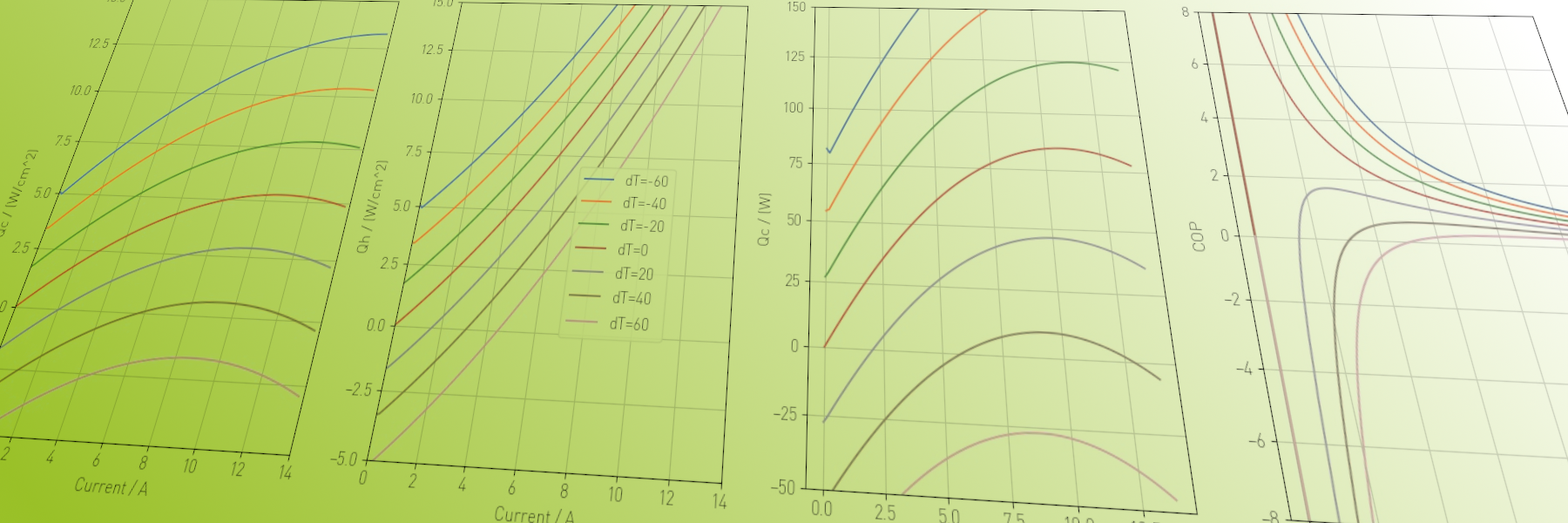
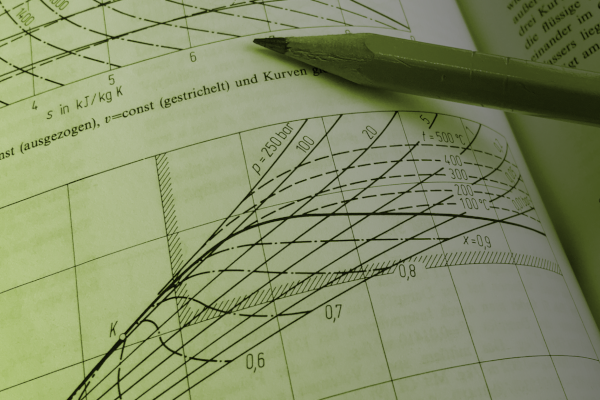
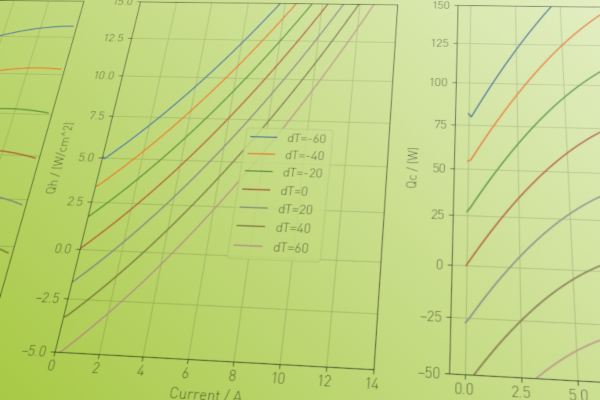
TRANSIENT LOW-ORDER MODELS
First principle modelling and dimensional analysis is the perfect tool to validate concepts and quantify the optimization potential. As the complexity of the models is kept simple at an initial phase but grows with the task, the approach is very efficient.
Transient physical models are the basis of a model-based approach in digital monitoring and diagnosis. Unlike a purely data-driven approach, a model-based setup works reliably and generate value even with very few data and limited observation time.
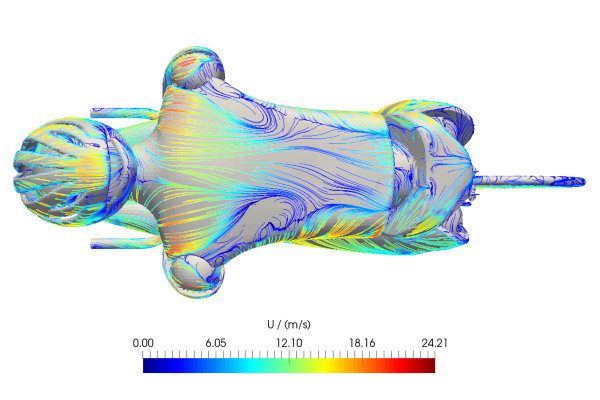
COMPUTATIONAL FLUID DYNAMICS (CFD)
CFD is a very powerful tool to analyze and optimize designs in fluid- and thermodynamics. It provides the full 3D dataset required to understand how the individual components and details contribute to the overall performance.
Assuming an incompressible fluid and steady-state conditions, simulations are a very time- and cost-effective tool. But as the complexity of the physics and geometry increases so does the effort to setup and run a simulation. I requires know-how and experience to find the right level of simplification and operate the CFD tool efficiently.
Through the AirShaper online aerodynamics platform, which automates such CFD simulations, this has become accessible also to the non-specialized engineer. As a partner of AirShaper, we invite you to try the AirShaper online simulation tool for a first evaluation of your design!
Our focus has accordingly shifted from setting up the simulations themselves towards helping you define the strategy of your simulation campaign and using those results to prepare more efficiently for your measurement campaign.
We are happy to discuss your application and help you find the best approach!
SENSOR SELECTION AND SIGNAL PROCESSING
As a simulation, a measurement tells only part of the truth. Measurements can be very costly and should only be considered after careful formulation of the problem statement selection of sensors and data acquisition.
Digital monitoring and diagnosis applications require a thorough understanding of the links between the parameters to be observed and the signal respective sensor signals. The selection of sensors influences deployment feasibility greatly. A bad choice can lead to non-detection or false alarms.
We help you to draw the right conclusions from the measurement signals.